Symmetry in DNA domains of Yeast chromosomes
Stanislaw Cebrat
Institute of Microbiology, University of Wroclaw
ul. Przybyszewskiego 63/77
e-mail: cebrat@angband.microb.uni.wroc.pl
Miroslaw Dudek
Institute of Theoretical Physics, University of Wroclaw
pl. Maxa Borna 9
e-mail: mdudek@ift.uni.wroc.pl
CONTENTS: ABSTRACT # INTRODUCTION
# RESULTS # DISCUSSION
# REFERENCES #
ABSTRACT We have shown that coding sequences
in DNA molecule are highly correlated and organized in a self-similar domain
structure in which the nucleotide triplet-antitriplet mirror symmetry in
the strand is preserved. The tendency to reach the symmetry forces the
specific organization of DNA molecule and generates long-range power-like
correlations in purines and pyrimidines distribution.
INTRODUCTION
Stanley et al. [1, 2] have discovered long-range, power law correlations
in sequences of nucleotides in DNA molecules. Occurrence of the correlations
has been next approved several times, but the nature of their generation
and causes are still obscure [1] -- [7]. The group of Stanley [1, 2] has
claimed, that the correlations could be found only in noncoding sequences
whereas coding sequences disturb their occurrence. Recently we have found
some DNA features which seem to explain previous findings in long-range
correlations. In particular, we have analyzed the Yeast chromosomes and
found that:
- the distribution of coding sequences is highly correlated [8], there
are long-range power-law correlations in their apparance,
- in general, the sense strands of coding sequences are richer in purines
than in pyrimidines [8, 9, 10],
- these both features generate long-range correlations in purines and
pyrimidines distribution [9].
The finding that sense strand of coding sequences tends to be richer
in purines means that there is an asymmetry between sense and antisense
strands of the coding sequences. This asymmetry has very important methodological
implications: the statistical analysis of DNA molecule has to be done in
separate strands of DNA molecule, absolutely with differentiating for sequences:
noncoding, coding in the analysed strand (sense) and coding in the complementary
strand (antisense). This means that one should take into consideration
not only if the sequence is coding but also how it is read what could be
very important, since there are strong correlations in the distribution
of nucleotides in specific codon positions. Statistical analysis of DNA
molecule organization without considering its logical structure has no
sense.
RESULTS
It has been found by Feldman et al. [11] that in Yeast chromosome II
(Ych2) genes are distributed in regions relatively rich in GC. Nevertheless,
recently Carels, Barakat and Bernardi [12] reported that the distribution
of coding sequences in human and maize genomes in respect to GC contents
of the region are different and that this is not because of gene base composition
but because of the composition of noncoding sequences. We have analysed
five Yeast chromosomes (1, 2, 3, 6, 11) and we have found that the ORFs
longer than 150 triplets (supposed to be coding) have higher GC content
and that noncoding sequences have lower GC content than average composition
chromosome. But the other striking feature of the Yeast chromosomes is
that the ratio of purines to pyrimidines in coding sequences is significantly
higher in the sense strand than in antisense strand of gene (especially,
high ratio [A]/[T]). Since the whole chromosome are rather well balanced
(differences between purines number and pyrimidines number in one strand
are below 1%) the asymmetry of coding seqences has to be compensated along
the DNA molecule.
Base composition of DNA strand should be reflected in its triplet composition
(we use the name triplet for all triplets independently of their position
in coding sequence).
We have found almost identical triplet composition for all five analysed
chromosomes and for all six phases for each chromosome. What is more important,
all these triplet compositions are significantly different from expected
abundance counted from the base composition of the DNA strands (Fig.
1).
We have observed the tendency to keep the same deviation from expected
value for any triplet and its complementary sequence (we called it antitriplet).
That is why we have divided all triplets into two groups - one group consists
of triplets rich in purines and the second one - complementary triplets
rich in pyrimidines. Each triplet of the first group corresponds to one
triplet of the second group. In the Fig. 2 we have
shown the abundance of triplets in phase 1 of the Ych2 strand W (stands
for Watson). Two plots represent triplets rich in purines and its complementary
sequences whereas the third and the fourth plots represent values counted
from the base composition of the strand. The observed striking symmetry
means that the chromosome is a specific dispersed palindrome - there exist
a sequence and somewhere in the same strand another sequence complementary
to the first one (!). Since such a symmetry can be found for the stochastic
sequence one could find it as trivial observation. However, in the chromosome,
the purine/pyrimidine distribution is significantly deviated from statistically
expected.
The significant differences in base composition of coding sequences
in comparison to noncoding sequences should be reflected in this specific
triplet/antitriplet symmetry. We have analysed these differences using
chi square values 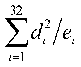 where:
where: 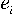 is the number of
specific triplet rich in purines and
is the number of
specific triplet rich in purines and 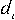 is the difference between the number of i-th triplet and a triplet
complementary to it. We have counted the chi square values for the whole
phases of chromosomes, sequences in Open Reading Frames (ORFs) longer than
150 triplets (presumed coding sequences) and for sequences which are outside
ORFs longer than 70 triplets (almost absolutely sure noncoding sequences).
Since the whole DNA phases are symmetrical, the asymmetry of coding sequences
has to be compensated somewhere along the strand. The compensation of coding
sequence in one strand could be done by a coding sequence lying in the
opposite strand. This could be possible if:
is the difference between the number of i-th triplet and a triplet
complementary to it. We have counted the chi square values for the whole
phases of chromosomes, sequences in Open Reading Frames (ORFs) longer than
150 triplets (presumed coding sequences) and for sequences which are outside
ORFs longer than 70 triplets (almost absolutely sure noncoding sequences).
Since the whole DNA phases are symmetrical, the asymmetry of coding sequences
has to be compensated somewhere along the strand. The compensation of coding
sequence in one strand could be done by a coding sequence lying in the
opposite strand. This could be possible if:
- the triplet composition of coding sequences is random, or
- there are general rules for triplet composition of all coding sequences
and there is a balanced coding function of phases and strands in chromosome,
or
- there is no general rule for triplet composition of coding sequences
but the distribution of these sequences is not random - it obeys the rule
of preservation the symmetry of DNA phase and strand, or
- the organisation of chromosome respects the rule of symmetry by both:
nonrandom coding sequence distribution and by compensation the disturbances
in the symmetry introduced by coding sequences with intervening noncoding
sequences.
The first possibility could explain the finding of Stanley's group [1,
2] that there are no long range correlations in coding sequences, but if
this possibility is true, the abundance of triplets in coding sequences
should correspond to the stochastic abundance of triplets counted from
the base composition, which is not the case.
The assumption that one of the other possibilities is true should implicate
that the compensation is a rule imposed in shorter distances than the whole
chromosome. We have checked this hypothesis counting the chi square values
for symmetry triplet/antitriplet for different parts of Ych2 and plotting
the triplets/antitriplets distribution. To cut properly the chromosome
we performed the random walk for coding capacity of Ych2 (shown in Fig.
3). The walker has moved along the chromosome and it is going up if
it is in the triplet coding in the strand W and down if it is in the triplet
coding in the strand C (stands for Crick). Otherwise it has been moving
horizontally.
We have divided the Ych2 into parts marked in the picture and next we
have analysed the parts for symmetry triplet/antitriplet. The standardized
values for abundance of triplets and their antitriplets have been plotted
in the Fig. 4. (each pair of the lines in the Fig.
4 representing different parts marked in Fig. 3.
differs from the preceding one by the added constant values 0.05 to get
clear presentation of the Figure). Notice, that there are two lines (!)
- for each X value two data are plotted - one for triplet rich in purines
and the second for triplet complementary to the first one, rich in pyrimidines.
The plot (B) represents the triplet and antitriplet composition of five
Yeast chromosomes (1,2,3,6, and 11), (A) - the whole W strand of Ych2.
The plot (d) represents the triplet and antitriplet composition of the
sequence of 2903 triplets what is less than 0,4% of the sequences represented
in plot (B). The plots (a) - (d) represent hierarchically ordered DNA domains.
The self-similarity od DNA is evident on large range of scales - the DNA
has appeared as a fractal. For each domain the chi square value for triplet/antitriplet
symmetry was up to two orders smaller than for differences between the
found codon abundance and its expected (stochastic) values.
In Fig. 5, the plots represent the symmetry
triplet/antitriplet in coding sequences (in ORFs longer than 150 codons).
The lowest pair of lines represents the codon composition of all ORFs longer
than 150 codons in strand W of Ych2. It is easy to notice, that the symmetry
of codon/anticodon is broken in the coding sequences. The second pair of
lines represents the sum of coding sequences of both strands, but read
in the strand W and in the direction of strand W. That means that in fact,
the coding sequences of strand C are represented by their complementary
sequences. Chi square value for triplet/antitriplet for both strands together
is more than two orders lower than for separate strands. Next two pairs
show, that the expected values of triplet abundance for nucleotide composition
of whole chromosome or for coding sequences are different from realy found
in coding sequences. That means that coding sequences of one strand compensate
the coding sequences of the another strand restituting the symmetry triplet/antitriplet.
Futhermore, this compensation is not connected with stochastic process
- the reached symmetry does not represent the expected (stochastic) triplet
abundance. The compensation can be even shown in very short sequences.
The three top plots represent the symmetry in short sequence (domain d
- the last 2903 codons of Ych2). The first represents coding sequence of
strand W, the second - coding sequence of strand C and the third one -
the whole sequence of strand W of the fragment.
DISCUSSION
To understand the organization of Yeast chromosome we have compiled
three findings:
- the longe-range power-like correlations in distribution of coding sequences
(proving that distribution of coding sequences along the chromosome is
not random),
- asymmetry of coding sequences and
- local symmetry in DNA molecules.
The nonrandom distribution of coding sequences has been proved by statistical
analysis of several Yeast chromosomes and by simulation of artificial chromosome
with superimposed rules resulting from this analysis, in which we have
succeeded in generating the distribution of ORF legth resembling the natural
chromosome [8, 9]. The asymmetry of coding sequence is trivial, since we
have found the simple asymmetry in nucleotide composition of sense and
antisense strand [10]. One can argue that the symmetry triplet/antitriplet
is just a result of stochastic rules, since the stochastic DNA with the
nucleotide composition of Ych2 is symmetrical. This would be true, nevertheless,
the stochastic DNA has a stochastic triplet composition while Ych2 has
triplet composition significantly deviated from the stochastic one but
still has preserved symmetry. We would like to stress, that symmetry triplet/antitriplet
is arbitrarely assumed by us, but in fact the symmetry could probably be
found in the sequences of different length.
There is another premise suggesting that symmetry is not the result
of stochastic compensation. This premise could be concluded from the data
collected by Karlin and Burge [13]. The abundance of dublets in many genomes
has specific features: there exist almost the same numbers of dublets and
their complementary sequences and the dublet abundance does not correspond
to the nucleotide composition of genome (what we have shown for triplets).
Sequences the most deviated from the expected ones are the palindromes
themselves (ApT, TpA, GpC, CpG). These dublets do not obey any rule of
symmetry because they are symmetrical themselves and they do not need to
be localy compensated. It has happened that these dublets play very important
and specific functions in expression of genetic information.
All these features of DNA molecules have important biological implications.
DNA molecule is not a facultative sequence of nucleotides just realizing
the demand of information transfer. If we imagine a DNA molecule in a cell
which does not need to transfer any information - the molecule would not
be a random one (has Stanley's group [1, 5] found it for noncoding sequences?).
We suggest that such a molecule would be a symmetrical one. The information
can be superimposed on this primary sequence but this is connected with
the destabilization of the molecule. The destabilization, if in long sequence,
has to be localy compensated and it seems that the compensation could be
done by preserving the dispersed palindromic symmetry of the sequence.
The compensation can be obtain by specific distribution of these "information
transferring sequences" along the strand, e.g. alternative coding
by both strands.
The assumption that the information transfer has a secondary role in
the organization DNA sequence has other implications. Since not every possible
sequence of nucleotides could be realized, only some of theoretically possible
sequences could be available by organisms and exploited by them. This could
be considered as a restriction imposed on organisms but it maybe also considered
as a mechanism which enables the evolution. It explains the famous Haldane
Dylemma [14, 15]. In 1937 Haldane showed that organisms have to pay for
maintaining active genes with elimination of harmful mutations. Taking
together the mutation rate and the size of genome, the cost of this elimination
seems to be unbearable and would exterminate the species.
Thus far, the only known mechanism of elimination of such mutations
has been the Darwinian selection operating on the phenotypic level. The
rules forcing the specific organization of DNA molecules into self-similar
and symmetric domains lead to the stabilization of DNA, but simultaneously
the number of possible molecular states is restricted. That means, that
forbidden states on the molecular level are not and do not have to be checked
by Darwinian, phenotypic selection and eliminated by genetic death.
REFERENCES
- C. K. Peng, S.V. Buldyrev, A.L. Goldberger, S. Havlin, F. Sciortino,
M. Simons and H.E. Stanley, Nature 356, 168-170 (1992)
- H.E. Stanley, S.V. Buldyrev, A.L. Goldberger, J.M. Hausdorff, S. Havlin,
J. Mietus, C. K. Peng , F. Sciortino and M. Simons, Physica A 191
1-12 (1992)
- R.F. Voss, Phys. Rev. Lett. 68, 3805-3808 (1992)
- R.F. Voss, Phys. Rev. Lett. 71, 1777 (1993)
- C. K. Peng, S.V. Buldyrev, A.L. Goldberger, S. Havlin, R.N. Mantegna,
M. Simons, and H.E. Stanley, Physica A 221180-193 (1995)
- Mark Ya. Azbel, Phys. Rev. Lett. 75, 168-171 (1995)
- A. Arneodo, E. Bacry, P.V. Graves and J.F. Muzy, Phys. Rev. Lett.
74 3293-3296 (1995)
- S. Cebrat and M.R. Dudek (1995) preprint IFT UWr August 893/95,
submitted to Phys. Rev. Letts. on August 24, 1995
- M.R. Dudek and S. Cebrat, preprint IFT UWr October 897/95,
submitted to Phys. Rev. Letts. on October 4, 1995
- S. Cebrat, M.R. Dudek and A. Rogowska, submitted to Yeast
- H. Feldmann + 96 coauthors, EMBL J. 13, 5795-5809 (1994)
- N. Carels, A. Barakat and G. Bernardi, Proc. Natl. Acad. Sci. USA
92, 11057 - 11060 (1995)
- S. Karlin and C. Burge, Trends Genet., 11, 283 - 290,
(1995)
- M. Kimura, The Neutral Theory of Molecular Evolution, Cambridge
University Press (1983)
- J.B.S. Haldane, Natural selection in Darwin's biological work,
ed. P.R. Bell, pp 101-149, Cambridge University Press (1959)
Document created and maintained by Jerzy Kakol. Last revised: 17.07.1996
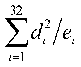 where:
where: 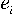 is the number of
specific triplet rich in purines and
is the number of
specific triplet rich in purines and 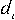 is the difference between the number of i-th triplet and a triplet
complementary to it. We have counted the chi square values for the whole
phases of chromosomes, sequences in Open Reading Frames (ORFs) longer than
150 triplets (presumed coding sequences) and for sequences which are outside
ORFs longer than 70 triplets (almost absolutely sure noncoding sequences).
Since the whole DNA phases are symmetrical, the asymmetry of coding sequences
has to be compensated somewhere along the strand. The compensation of coding
sequence in one strand could be done by a coding sequence lying in the
opposite strand. This could be possible if:
is the difference between the number of i-th triplet and a triplet
complementary to it. We have counted the chi square values for the whole
phases of chromosomes, sequences in Open Reading Frames (ORFs) longer than
150 triplets (presumed coding sequences) and for sequences which are outside
ORFs longer than 70 triplets (almost absolutely sure noncoding sequences).
Since the whole DNA phases are symmetrical, the asymmetry of coding sequences
has to be compensated somewhere along the strand. The compensation of coding
sequence in one strand could be done by a coding sequence lying in the
opposite strand. This could be possible if: